1. Verifiering av den fysikaliska principen för kärnformeln
Lagen om massans bevarande
Alla formler är baserade på den fysikaliska naturen hos m=ρ×V (massa = densitet × volym)
Densitetsvärde
Teoretisk densitet för rent aluminium: 2 698 kg/m³ (20℃)
Det ungefärliga värdet på 2 700 kg/m³ är rimligt för industriella beräkningar (fel < 0,1 %)
2. Verifiering av geometriska formlers noggrannhet
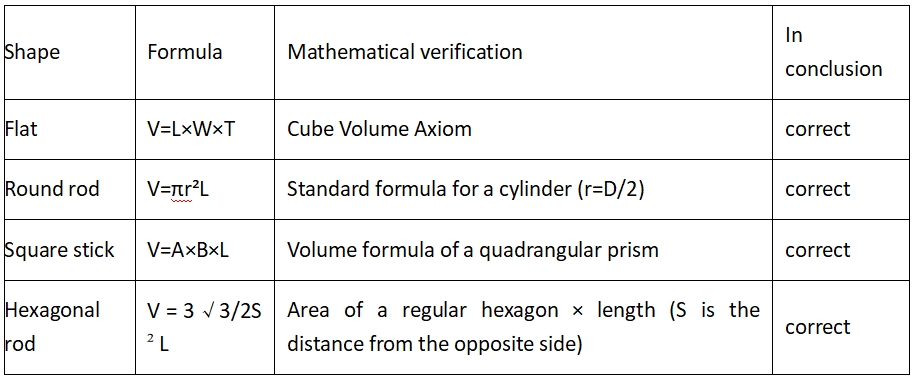
2.1. Standardformel för geometrisk volym
Begränsningar för formeln för fyrkantiga rör:
Detta gäller när rörets väggtjocklek är jämn och den inre vinkeln är rätvinklig (det faktiska fyrkantiga röret har en rundad övergång och det teoretiska felet är cirka 1–3 %)
3. Verifiering av enhetssystemkonsekvens
Riskpunktsundersökning för beräkning över flera enheter
4. Ändring av teknisk lämplighet
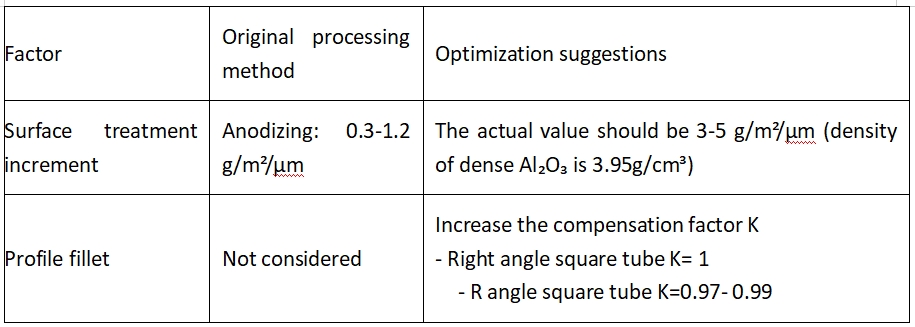
4.1. Kompensation för icke-ideala faktorer
4.2. Kvantifiering av toleranspåverkan
Tjocklekstolerans ±10% → Viktavvikelse ±(8% ~ 12%) (tunnväggiga delar är känsligare)
Lösning: W faktiskt = W teoretiskt × (1 + Δt / t) (Δt : tjockleksavvikelse)
5. Randvillkorstest
Verifiering av extremfall:
Scenario med densitetsanomali
7xxx-legering (7075): Uppmätt densitet 2,810 g/cm³ → Om 2,7 g/cm³ används av misstag är felet +4,1 %.
Formeltabell
4t(A + B) - 4t² är en standardmässig ingenjörsberäkning som beräknas genom att multiplicera sektionens omkrets med väggtjockleken och sedan subtrahera de fyra hörnen.
Beräkningsexempel:
1.6061 aluminiumplåt(1000 × 500 × 10 mm, längd 2 m): B = 1000 × 500 × 2 × 0,0027 = 27 kg
2,7075 runt rör(ytterdiameter 50 mm, väggtjocklek 3 mm, längd 1,5 m): W = [(50-3)×3×3,1416×1,5]×0,00283 ≈ 5,65 kg
3. Fyrkantigt rör(40×40×2 mm, längd 3 m): B = [2×2×(40+40-4)×3]×0,0027×0,98 ≈ 2,42 kg
Rekommenderat arbetsflöde
1. Välj densitet → 2. Mät verklig storlek → 3. Välj kompensationsfaktor → 4. Beräkna med formel
Publiceringstid: 17 juni 2025